| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 계수정렬
- 기러기목
- 솔딱새과
- 딱다구리과
- 비둘기목
- AI역량평가
- Python
- 딥러닝공부
- python3
- IBK기업은행 인턴
- 오리과
- ADsP
- 한국의 새
- structured_array
- Birthday paradox
- 직박구리과
- SimpleCraft
- django
- 비둘기과
- keras
- 흰날개해오라기
- 생일문제
- 맑은소리 스피치학원
- 가마우지과
- 한국의새
- 참새과
- 참새목
- AI전략게임
- 딥러닝 공부
- 백로과
- Today
- Total
진박사의 일상
[컴퓨터보안] 2강 - 2장 Cryptographic Tools 본문
Cryptographic Tools
Symmetric Encryption(대칭키 암호화)
conventional encryption(고전 암호화) or single-key encryption(단일키 암호화) 라고도 함. 공개키 이전의 대응
2개의 요구조건
- 안전한 암호화 알고리즘
- 보낸자와 받는자의 secret key(단일키)의 copy를 안전하게 나눠 가지고 저장하는 기술

평문(Plaintext) X 입력 -> 암호화 알고리즘(ex DES)) + 비밀키(K0 -> 암호문(Cipertext) Y=E[K,X] 전송 -> 복호화 알고리즘 + 비밀키(K) -> X = D[K,Y] -> 평문 출력
대칭키 암호화 공격방법
- Cryptanalytic Attacks : 암호(알고리즘) 분석 - 일반적으로 암호 알고리즘은 공개해서 여러 사람에게 취약점 분석, 평문의 특징 분석 - 가장 많이 쓰는 알파벳 e나 th 등으로 치환, 평문-암호문 쌍을 통해 key 분석 -> 평문이나 key를 찾기
- Brute-Force Attacks : 가능한 모든 key를 시도. 절반정도 시도하면 대부분 성공.(key 사이즈에 따라 걸리는 시간 다름)


DES - FIPS PUB 46 발표, 56bit-key -> 1998년 깨짐
Triple DES - DES key를 2 or 3개 사용해 key 길이를 늘려 brute-force 방지 - 단점은 너무 느리고 성능 저하
AES - NIST에서 발표. 3DES보다 안전, 효율적, 대칭키, 128bit block size에 128/192/256bit key -> 2001년 FIPS 197 발표
암호화 방법 분류 - 각각 독립적인 차원으로
- 작업의 종류 - Substitution(치환), Transposition(위치 변경) -> 둘 다 번갈아 사용하면 효과적
- key의 종류 - 단일키-Symmetric, 다중키-Asymmetric
- 데이터 처리 방법 - Block Cipher(블럭 기준 - DES, AES 등), Stream Cipher(패킷 전송시 한 바이트 씩 연속적으로)
Cryptanalytic Attacks 공격 타입
Ciphertext(암호문) only : 암호화 알고리즘 + 암호문 알고 있는 상태
Known plaintext(평문) : 암호화 알고리즘 + 암호문 + 일부 암호문-평문 쌍을 알고 있음
Chosen plaintext : 암호화 알고리즘 + 암호문 + 공격자가 선택한 평문에 대한 암호문을 알고 있음.
Chosen ciphertext : 암호화 알고리즘 + 암호문 + 공격자가 선택한 암호문에 대한 평문을 알고 있음.
Chosed text : Chosen plaintext + ciphertext
일반적으로 Chosen plaintext 정도까지 막을 수 있다면 안전하다고 판단
Computationally Secure Encryption Schemes
암호화가 Computationally Secure하다 = 정보의 가치보다 암호를 깨는 비용이 크다, 암호를 brute-force로 깨는 시간이 정보의 유효 시간보다 길다. (ex. 사람의 주민번호를 알아내는데 몇백년이 걸릴 때 Computationally Secure)
Feistel Cipher Structure

Block Cipher Structure
대칭 블록 암호 : 일련의 라운드, key로 Substitution과 Permutation으로 컨트롤됨.
디자인해야 할 특징 : 블록 사이즈, 키 사이즈, 라운드의 횟수, Subkey 생성 알고리즘, Round Function(F), 빠른 암호화/복호화 소프트웨어, 쉽게 분석할 수 있게
DES(1977~1997) : Feistel network의 마이너 버전
3DES - 각각 다른 key로 암호화 할때는 암호화-복호화-암호화 순으로 복호화 할 땐 복호화-암호화-복호화 순으로 -> 이렇게 했을 때 key를 전부 동일하게 설정하면 DES처럼 쓸 수 있음.(DES와의 호환성 위해) - 느림
AES : Expand key는 서브키 생성 알고리즘, 하나의 라운드는 [Substitute bytes] -> [Shift rows] -> [Mix columns] -> [Add round key] 네개의 연산으로 이루어짐. ※ 첫번째 연산에는 [Add round key]가 있고 마지막 round에는 [Mix columns]가 없이 연산 3개 뿐이다. 복호화 할때는 역순으로. [Substitute bytes]와 [Shift rows], [Mix colums]와 [Add round key]는 상호 교체 가능.

[Substitute byte] - S-box 테이블(암호화) <-> Inverse S-box(복호화) 을 이용해 전환
[Shift rows] - 하나의 칼럼에서 독립된 바이트를 다른 칼럼으로 전파
[Mix Columns] - 한 컬럼의 4개의 바이트로 새로운 바이트를 만들기
[Add round key] - expanded key와 XOR bit 연산
대칭키의 실질적인 보안 이슈
같은 키를 쓰기 때문에 평문를 유추가 가능한 ECB(electronic codebook) mode이 가장 간단한 multiple-block 암호화에 대한 접근 방식 -> mode of operation : 같은 평문과 같은 키를 사용해도 다른 암호문이 나와 ECB의 취약점을 보완
Mode of operation
Electronic Codebook(ECB) - 가장 간단. 코드북 - 같은 평문+ 같은 키 -> 같은 암호문이 나오므로
Cipher BLock Chaining(CBC) - XOR연산 특징을 이용해 블럭을 암호화 할 때 이전 블럭의 결과값을 체인처럼 연결해 다른 값이 나오도록 처리. 마지막 CN값만 저장하고 있으면 중간에 평문이 위조되었는지 파악 가능. / 단점은 전송 중 단 한 bit라도 잘못 전송되면 이후로 계속 전송되어 에러가 계속 전파.
Cipher Feedback(CFB) - 암호화된 결과와 평문을 XOR한 것을 시프트 레지스터를 통해 일정 비트씩 다음에 피드백 전송(체인처럼) 미리 암호화 연산을 해 두고 시간 단축. 특징 - 복호화에도 암호화 알고리즘 사용
Output Feedback(OFB) - CFB랑 유사한데 XOR 하기 말고 전송 - Encription을 미리 연산해둘 수 있는 장점.
Counter(CTR) - 랜덤한 카운터값을 정해서 카운터를 증가시켜가며 평문과 XOR. 장점 - 첫번째 counter만 알면 나머지 카운터값도 알 수 있으므로 한번에 병렬적으로 처리 가능
---- 9월 6일차까지
Block Cipher Encryption vs Stream Encryption
-Block Cipher Encryption : 평문을 block단위로 쪼개 암호화 - 키 재사용 - 큰 파일 암호화
- Stream Encryption : 입력이 Byte Stream 단위로 입력, Key값과 XOR 연산을 통해 암호화, Key도 Stream으로 제공 (한 byte씩 암호화 - 훨씬 빠름) - 패킷과 같이 간헐적으로 발생되는 스트림에서 사용 - Pseudorandom number 생성기(유사 난수이므로 일정 주기로 중복값 생성)로 key Stream을 생성 -> 디자인 시 고려할 점 : 암호화 키가 반복되는 주기가 길어야 함. 되도록 진짜 랜덤에 유사하게, 충분히 긴 key가 필요
Message Authentication(메세지 인증) - 메세지가 위변조 되지 않았는지 확인
- Active attacks에 대응, 수신된 메세지가 진짜인지(변경x, 확실한 출처인지, 시간적으로 정확한지(replay 공격 방지)), conventional 암호화를 사용 가능(전송자, 수신자 키 공유) -> but 좀더 효과적인 방법 없나?
Message Authentication Codes(MAC)
key와 MAC 알고리즘을 통해 MAC code를 붙여서 전송하고 수신 측에서 떼어넨 것과 수신측 MAC 알고리즘을 통해 얻은 MAC 코드를 비교 - MAC 알고리즘으로 해시
Secure Hash Function - 가변길이의 message를 입력받아 고정 길이의 Hash value를 생성
입력 길이가 출력 값보다 훨씬 길기 때문에 출력 값에 중복이 생길 수 있음 -> Collision 발생

(a) conventional encryption 사용 - 위 설명과 동일
(b) public-key encryption 사용 - 서로 다른 한 쌍의 키를 사용
(c) secret value 사용 - 메세지 양 끝에 키를 붙이고 Hash에 넣어 나온 값을 mac으로 전송해 비교. (수신측도 동일하게)
Hash 함수의 조건
- 입력은 어떤 길이라도 상관 없어야 하고 출력은 항상 고정 길이
- x값이 주어지면 H(x)값을 구하기 쉬워야 하고 반대로 H(x)=h 가 있을 때 h로부터 x를 유추가 Computationally 불가능 해야 한다.(One-way resistant)
- Second pre-image resistant or Weak collision resistant -> x값을 알 때 H(x) = H(y)인 y값을 찾는 것이 Computationally 불가능 해야 한다.
- Collrision resistant or Strong collision resistant -> H(x) = H(y)인 어떤 x값과 y값의 쌍을 찾는 것도 Computationally 불가능 해야 한다.
Security of Hash Functions(Algorithm) (SHA)
NIST가 개발. SHA가 널리 사용되는 hash 알고리즘 (전에는 MD5였는데 조건이 깨져서 사장됨)
1993년 FIPS 180으로 출판. 1995년 SAH-1, 2002년엔 FIPS 180-2, 출력 길이에 따라 SHA-256, SHA-384, SHA-512
-공격법 - Cryptanalysis(해시 알고리즘의 취약점 이용), Brute-force
-사용법 - 패스워드(패스워드 자체x 해시만 저장), 침입 감지(파일의 hash를 저장해두고 비교해 위변조 일어났는지 확인)

Birthday Attack - Birthday Paradox(23명정도 모이면 생일이 같은 사람이 있을 확률이 50% 이상 -> 특정 범위가 2^n 승일 때 2^(n/2)개를 뽑으면 같은 숫자가 나올 확률이 50% 이상)을 이용한 공격
SHA-3 - 보안/비용/구현 특징 등을 고려해 2015년 발표
HMAC - MAC을 만드는데 안전한 cryptographic hash code(빠르게 동작)를 이용하도록 정의. 라이브러리 코드가 널리 이용가능, key값에 의존하지 않음 -> TLS나 IP 보안 등에도 사용. 공격자가 Collision을 찾는데 O(2^(n/2))만큼 걸림.
-조건 : Hash함수를 수정x, 원래 수행 능력 유지, 새로운 해시 함수가 나오면 잘 적용할 수 있어야 함, key값 처리가 간단, 분석하기 쉽게 만들어야 함.

Public-key Encryption(공개키 암호화) Structure
1976년 Diffie and Hellman에 의해 제창. 수학적 함수에 기반, 비대칭한 2개의 키를 사용, public key는 공개 private key는 비공개. 공개키를 어떻게 공개할지 프로토콜이 필요

(a) 공개키를 통한 암호화 : 공개키 링에서 전송할 사용자의 공개키를 가져와 암호화해서 전송 -> 수신측에서 본인의 개인키를 사용해 복호화
(a) 개인키를 통한 암호화 : 개인키를 이용해 암호화해서 전송 -> 수신측에서 발신측의 공개키를 검색해 복호화 -> 그러나 그 암호문이 누출되면 다른 그 누구도 복호화 할 수 있지 않나? -> 그래서 주로 사용되는 것은 '해당 암호문이 발신측에서 보낸 것이 확실하다' 라는 것을 증명하는 디지털 서명 기술에 활용
좋아보이는데 왜 AES같은 대칭키를 더 많이 사용하나? -> 대칭키가 훨씬 성능이 좋음
공개키 알고리즘 종류
RSA - 디지털 서명(O), 대칭키 배포(O), 비밀키 암호화(O)
- 1977년 Rivest, Shamir, Adleman에 의해 개발, 현재까지도 가장 많이 사용, 메세지를 숫자로 계산해서 처리
Diffie-Hellman - 대칭키 배포(O) - 키 교환에 제한적 이용
DSS(Digital Signature Standard) - 디지털 서명(O) - SHA-1과 함께 전자 서명에만 사용
ECC(Elliptic Curve Cryptography) - 디지털 서명(O), 대칭키 배포(O), 비밀키 암호화(O)
- RSA보다 key 길이가 짧아 계산량-, 키 찾기는 조금 어려움
공개키 암호화의 요구조건 - 모두 만족은 RSA와 ECC밖에 없음
- Computationally하게 key 쌍을 만들기 쉬움
- Computationally하게 public key를 가지고 평문을 암호화가 쉬움
- Computationally하게 private key를 가지고 암호문을 복호화가 쉬움
- Computationally하게 public key로부터 private key를 찾는 것이 불가능
- Computationally하게 key 없이 암호문으로부터 original message를 찾는 것이 불가능
- (Optional) public key와 private key의 역할이 상호 교체 가능
RSA
- 정수의 지수승으로 소수를 나눠서 이용
- 암호화 : C = M^e mod n, 복호화 : M = C^d mod n = (M^e)^d mod n
- 여기서 n과 e 값은 공개키로, d 값은 개인키로 사용 ( 공개키 PU={e, n}, 개인키 PR={d,n} )
- 키 생성 : (1) 서로 다른 소수 p, q를 구함. -> (2) n = p*q 구함 -> (3) Φ(n) = (p-1)*(q-1) = n에 대한 서로소의 개수? -> (4) Φ(n)와 서로소 관계이고 Φ(n)보다 작은 e를 구함 -> (5) d*e mod Φ(n) = 1이 되는 d를 구함 -> (6) 공개키 PU={e, n}, 개인키 PR={d,n}

실제로 한번 해봤다 RSA!
Key Generator 과정
7 11
n = 77
Φ(n) = 60
e = 7
d*7 mod 60 = 1...
d = (n*60 + 1) / 7이자 정수...
61 121 181 241 301(O)
d = 301 / 7 = 43
KU = {7, 77}
KR = {43, 77}
Encryption
M < n(=77) -> M = 70
C = 70^7 mod 77 = 49
Decryption
C = 49
M = C^d mod n = 70
오오 된다
현재 기술로는 n값은 1024bit 이상(300자리수)으로 추천 -> 무척 느림!
Security of RSA
- Brute force : 모든 가능한 private key를 시도. 막기 위해서는 긴 key space를 사용(하면 수행 속도 감소)
- Mashmatical attacks : 두개의 소수의 곱을 인수분해해야 함. -> 300자리 이상의 숫자를 2개의 소수로 인수분해?? ㄷㄷ
- Timing attakcs : 복호화 알고리즘에서 지수승 연산 작동되는 시간을 분석해서 bit별 속도 차이로 분석 - 대응법 : 랜덤 delay 주기, 지수 연산에 걸리는 속도 일정하게
- Chosen ciphertext attacks
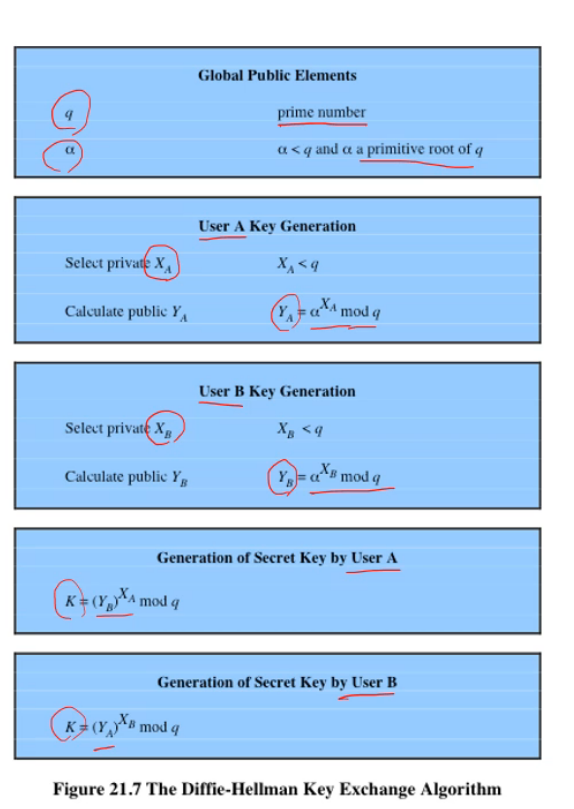
Diffie-Hellman Key Exchange
1976년 개발, 공개키 암호화 알고리즘으로 나왔지만 깨져서 현재는 key 교환에만 사용. 이산로그 계산의 복잡성을 이용
순서 - 소수 q와 q의 primitive root(원시근) α을 구함. q와 α는 공개키 -> User A는 랜덤 Xa를 골라 Ya = α^Xa mod q라는 값을 계산 -> User A는 랜덤 Xb를 골라 Yb = α^Xb mod q라는 값을 계산 -> 그리고 Ya와 Yb를 교환 -> 유저 A는 Yb^Xa mod q = K를, 유저 B는 Ya^Xb mod q = K를 같이 구함 -> 공격자는 K값을 로그 연산으로 풀기 어려움
Man-in-the-Middle Attack - 통신 중간에 끼어들어서 대신 전송받음 - 서로에게 받은게 맞는지 확인 필요
DSS - SHA-1 해시 함수를 이용.
디지털 서명
- 출처와 데이터 무결성에 대한 인증에 사용가능
- 문서를 해시로 암호화한 것을 비밀키로 삼아서 전자 서명 - 변경될 경우 변경된지 알 수 있음.
- 문서 자체를 암호화 하지 않았다면 Confidentiality(기밀성)은 제공하지 않음.
- public key가 진짜 그 사람의 public key가 맞는지 확인 필요

Public Key Certificates(공개키 증명)
원 데이터(bob의 id + 공개키 + CA 정보) -> 해시 -> CA의 개인키로 암호화해서 원 데이터에 서명으로 첨부
-> if 원 데이터 -> 해시 == 서명 -> CA의 공개키로 복호화: then 증명 완료
CA의 공개키를 증명하기 위해서는 다른 CA와 체인처럼 연결되어서 증명 - top level은 OS 자체에서 하드코딩
- CA(Certificate Authority)
Key Distribution(키 분배) 방법 A->B
1. 물리적으로 만나서 전달한다.
2. 믿을만한 제 3자(third party C)에게 전달해서 물리적으로 전달 C = Key distribution center
3. A와 B 사이에 이전에 사용하던 key가 있다면 그 key를 기반으로 새로운 key를 만들 수 있음.
4. 믿을만한 제 3자 C와 A 간, C와 B 간에 믿을만한 암호 연결이 있다면 C가 A와 B에게 key 배달 가능.

Kerberos Overview - defacto standard(비공식 표준)

Kerberos의 AS에 티켓 허가 요청 -> 티켓(24h 유효)과 세션키를 받아 TGS에 서비스 요청 -> 티켓(1h 유효)과 세션키 받아 service 요청 가능
Kerberos Realms(왕국) - 관리 주체가 다를 경우 다른 Realm끼리 요청 주고 받기

Kerberos의 Performance Issue
- Large scale이라도 성능이 좋다.
- 관리적인 측면에서 여러 Realm을 이용하는 것이지 성능 측면이 아니다
CA(Certificate Authority)
- 인증서 : public key + 키 주인의 User ID + CA가 서명한 문서가 인증서

Certificate Revoation List(CRL) : 인증 기간이 만료된 인증서 관리
Public key Infrastructure X.509(PKIX)

인증 기간이 만료되거나 신규 발급시 이전 인증서는 CRL에
인증서를 검증할 때 CRL도 가져와서 유효한 인증서인지 확인
PKIX Management Function : registration, initialization, certification, key pair recover, key pair update, revocation request, cross certification
Roter Machines - 세계 2차 대전때 만들어진 독일 Enigma, 연합군 Hagelin, 일본 Purple 등의 기반
substitution cipher를 복잡하게 해서 구현. 여러 실린더를 통해 치환. slow, medium fast의 3실린더라면 26^3 알파벳
'프로그래밍 > 공부' 카테고리의 다른 글
| [데베시] 2강 (0) | 2021.09.16 |
|---|---|
| 빅데이터 가명익명조치기술 전문 교육 1일차 (0) | 2021.09.14 |
| [컴퓨터보안] 1강 - 1장 Computer Security (0) | 2021.09.12 |
| [데베시] 정리 1차시 (0) | 2021.09.07 |
| 컴퓨터 일반 요약 공부 - Part 1. -1- (0) | 2021.09.01 |


